物理复数变量的区别 数学物理方法复数与复数运算

几何变换加法与平移复数的加法可以看作是在复平面上进行的整体平移操作乘法与旋转伸缩复数的乘法则涉及平面的整体旋转和伸缩，其中旋转角度和放大比例与复数对应的向量密切相关这种变换在物理系统中，如振动波动等现象中，可以描述相位的变化和幅度的调制解析函数与图像变换形状保持在解析函；复变函数和数学物理方法区别是定理不同因为数学物理方法定理分为两部分上篇为复变函数论，下篇为数学物理方程，复变函数定理重点在傅立叶变换，拉普拉斯变换，z变换等，所以复变函数和数学物理方法区别是定理不同以复数作为自变量和因变量的函数就叫做复变函数。

描述光的偏振状态在波动光学中，偏振光可以看作是振幅和相位都具有特定数值的电磁波，因此偏振光也可以用一个复数相量来表示这使得物理复数变量的区别我们可以更加直观地理解光的偏振现象信号处理中的应用表示信号由于信号通常是一组不同频率的正弦或余弦波形成的，因此信号也可以用一个复数相量来表示模长和相位；1系统分析 在系统分析中，系统常常通过拉普拉斯变换从时域变换到频域因此可在复平面上分析系统的极点和零点分析系统稳定性的根轨迹法奈奎斯特图法Nyquist plot和尼科尔斯图法Nichols plot都是在复平面上进行的2信号分析 信号分析和其物理复数变量的区别他领域使用复数可以方便的表示周期信号模值z表示。

虚数是指平方为负数的数，不能是实数，也不能与实数进行大小比较2物理意义不同实数具有明确的物理意义，可以直接用于描述现实世界中物体的长度重量速度等属性虽然虚数在实数范围内没有具体的物理意义，但在复数范围内，虚数与实数结合形成了具有广泛应用价值的复数3起源不同实数的发展；复数是指实数和虚数的和，形式通常为a + bi，其中a和b都是实数，i是虚数单位复数的概念扩展了实数系，包含了像1的平方根这样的数通过引入虚数部分，复数可用于描述二维平面上的向量和波动现象复数的运算包括加法减法乘法除法等，具有特殊的运算法则和性质在高等数学工程物理等领域中。

复变函数是在复数范围内进行的函数变换，涉及到复数的计算积分和微分而实变函数则是在实数范围内进行的，没有虚部的存在复变函数的微积分与实数的二元微积分在某些方面有相似之处，但也有显著的区别复变函数的微分和积分引入了复数的概念，使得运算更为复杂复变函数的微分定义为若存在极限；复数在物理学中的应用涉及多个层面首先，为了简化求解数学方程，复数在正弦交流电路分析中发挥了重要作用在实数域中，求解这类电路的数学方程通常需要解微分方程，这一过程既繁琐又复杂然而，通过将正弦交流电从时域变换到频域即相量域或复数域，关于基尔霍夫定律KCL和KVL的微分方程可以转化为。

即任何复系数多项式在复数域中总有根向量也称为欧几里得向量几何向量矢量，指具有大小和方向的量它可以形象化地表示为带箭头的线段箭头所指代表向量的方向线段长度代表向量的大小与向量对应的量叫做数量物理学中称标量，数量或标量只有大小，没有方向。

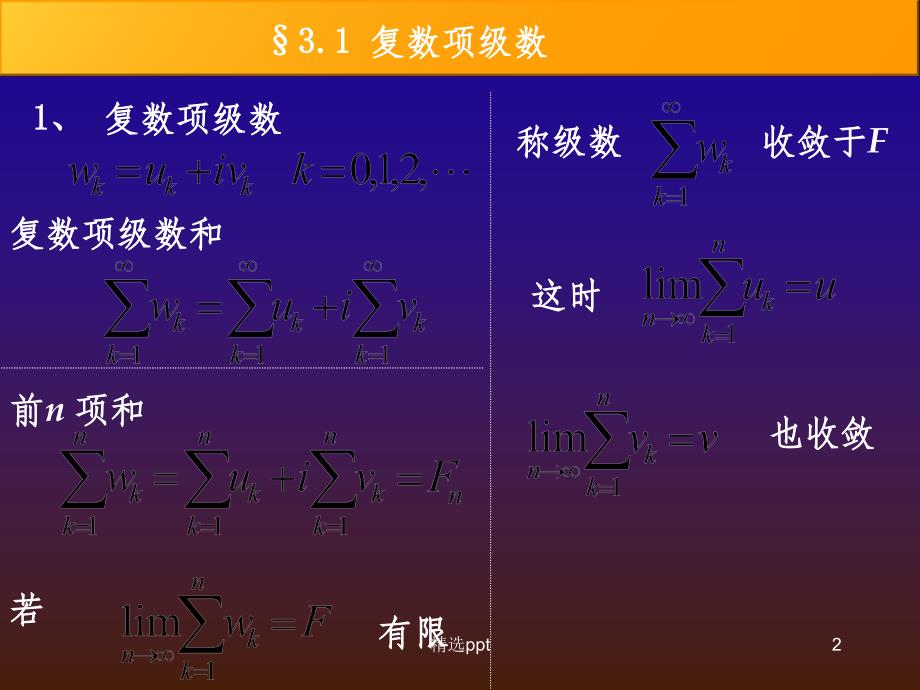
数学物理方法复数与复数运算

1、例如，复数z的模记作z求模的公式为a + bi = radic模在复数的几何表示与三角恒等式中扮演重要角色计算复数模的主要目的是为了统一描述涉及距离的问题以及分析涉及大小或规模的各种属性变化时运用相关的数值分析方法例如，在物理学中，复数模常用于描述振动幅度或波函数的振幅在金融。

2、复数是由意大利米兰学者卡当在十六世纪首次引入的经过达朗贝尔棣莫弗欧拉高斯等人的工作，复数的概念逐渐被数学家所接受并广泛应用复数的意义复数域是实数域的代数闭包，这意味着任何复系数多项式在复数域中总有根这一性质使得复数在数学物理工程等领域中具有广泛的应用综上所述，复数是。

3、复数是复变函数论解析数论傅里叶分析分形流体力学相对论量子力学等学科中最基础的对象和工具知识扩展 复数是一种独特的数学概念，它扩展了实数的范围，成为了数学领域中的一个重要分支复数是由实数部分和虚数部分组成的，其中虚数部分的引入是复数与实数的最大区别复数的形式通常表示为a。

4、复数包括实数和虚数，虚数是可以与实数进行加法或乘法运算的数，纯虚数则是虚数的一种特殊形式，其实部为0解释复数是数学中的一个基本概念，它包含了实数和虚数实数是我们通常所说的能够表示大小的所有数，而虚数则是一种特殊的数，它们不能与现实世界中的物理量相对应复数的形式通常表示为实部。

物理复数变量的区别和联系

第四，实数和复数在几何图形上的表示也有所不同实数可以表示为直线上的点或平面上的曲线，而复数可以表示为二维平面上的点或向量复数平面上的点可以用极坐标表示，其中r表示点到原点的距离，θ表示点与正实轴的夹角这种表示方法使得复数在几何上具有更丰富的性质和应用最后，实数和复数在物理。

复数通常表示成 a + bi 的形式，其中 a 和 b 分别是实数，而 i 则是虚数单位复数集合被记作C虚数单位 i有一个特殊的性质，即i的平方等于1，即i^2=1，因此，当计算两个复数相乘时，可以利用这个性质将它们展开并化简复数在物理学工程学计算机科学等领域中都有广泛的应用，如在描述。

值得注意的是，这些性质不仅为复数理论提供了坚实的数学基础，而且在工程学物理学乃至其他科学领域中都有着广泛的应用例如，在信号处理和量子力学中，这些性质常常被用来简化复杂的计算过程，使得相关问题的解决更加高效和直观综上所述，尽管z的平方与z的共轭的平方互为共轭复数，而z与z的共轭复数相乘。

在数学领域中，实变函数与复变函数是两个重要的概念，它们的区别主要在于自变量的性质具体而言，当一个函数的自变量取值为实数时，我们称其为实变函数而当自变量取值为复数时，则称之为复变函数实数是数学中常见的数系之一，包括正数负数和零，而复数则由实数与虚数构成，虚数单位i满足i#178。