线性回归与逻辑回归的主要区别如下适用场景线性回归主要用于预测连续型因变量Y线性回归逻辑回归区别,即定量输出例如线性回归逻辑回归区别,预测明天的温度或某人的考试成绩逻辑回归主要用于处理离散型因变量Y,特别是二元分类问题例如,判断考试是否及格或预测某事件是否会发生模型假设线性回归假设自变量X与因变量Y之间存在线性关系。
逻辑回归与线性回归的主要区别如下任务类型线性回归主要用于回归任务,即预测连续数值型数据逻辑回归专注于分类问题,尤其是二分类任务,通过非线性映射提供概率性分类结果输出形式线性回归预测值是连续的,可以是任意实数逻辑回归通过sigmoid函数将线性回归的结果映射到0到1之间,输出的是。
分类变量为因变量,连续变量为自变量,做逻辑回归或者是分类变量为自变量,连续变量为因变量,而且是做线性关系,则先将分类变量设置虚拟变量,再做线性回归线性回归通常是人们在学习预测模型时首选的技术之一在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。
1线性回归是预测模型中最知名的技术之一通常在学习预测模型时,线性回归是首选技术这种技术中,因变量是连续的,自变量可以是连续的或离散的,回归线的特征是线性2逻辑回归用于计算“事件发生”与“事件未发生”的概率当因变量是二元10, 真假, 是否类型时,逻辑回归是适用的3。
与线性回归的区别逻辑回归与线性回归在方法论上有显著区别线性回归通常借助最小二乘法解决,通过最小化误差平方和来拟合数据,适用于回归问题而逻辑回归则依赖最大似然法,即寻找使样本数据出现概率最大的参数估计,适用于分类问题最大似然法逻辑回归使用最大似然法来进行参数估计这种方法基于。
线性回归与逻辑回归的区别 线性回归和逻辑回归的主要区别在于它们处理输出变量和拟合函数的不同线性回归适用于连续值输出,而逻辑回归适用于二分类问题,其目标是估计类别的概率逻辑回归通过拟合概率为1类样本的条件概率来建立分类决策边界这使得逻辑回归能够提供概率预测,而线性回归提供的是连续值预测。
逻辑回归的白话解读及关键知识点原理逻辑回归虽然名字里有“回归”,但实际上用于分类任务它通过Sigmoid函数将预测值转化为01之间的概率,帮助我们判断结果属于哪一类Sigmoid函数可以将任意值映射到0和1之间,通过调整阈值进行分类判断与线性回归的区别逻辑回归本质上是广义线性回归的一种,形式与。



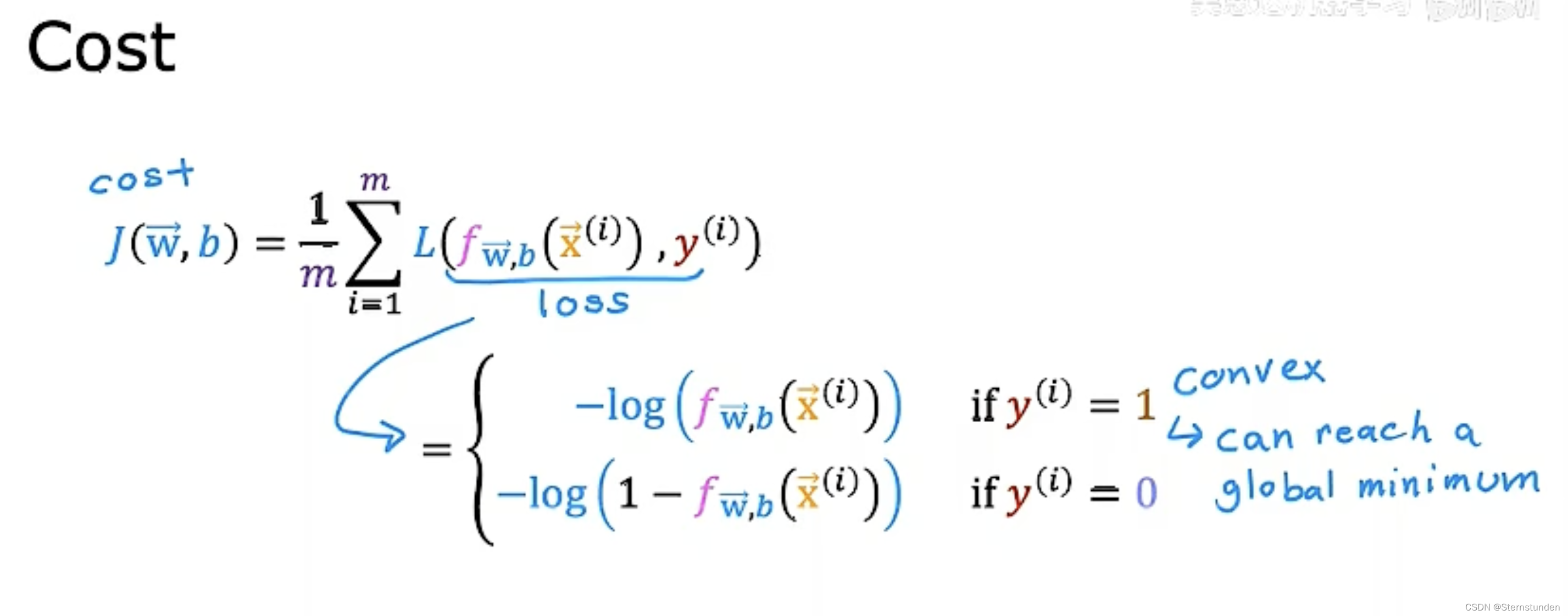







还没有评论,来说两句吧...