区别1“等于”一般情况下等于恒等区别的有条件的等于恒等区别,需要满足一定的条件等于恒等区别,才能成立2而“恒等于”则是无条件的,任何情况下都成立3所以,fx恒等于x^2+x,则不论x为多少,都成立而x^2+x不能说恒等于0,因为只有在x=0或-1时才成立对补充问题的解答一般来说,有两种情况会使用“恒等于。
恒等是存在变量时,无论变量取何值,等号左右两边总是相等两者的区别在于使用“恒等”时,式子中存在变量使用“等于”时式子中都是常量。
数学中等于与恒等的区别在于条件与普遍性等于代表条件等式,需要特定条件下变量满足的关系才能成立举例来说,等式 公式 只在满足条件 公式 时成立而恒等对应绝对等式,表示无论变量在允许范围内取值,等式总是成立如 公式 对所有 公式 都适用理解这点,我们知道几。
探索数学奥秘等于与恒等的微妙差异在数学的广阔领域中,符号等于与恒等虽然看似相似,却蕴含着深刻的逻辑与性质首先,让我们聚焦于等于,它如同一道桥梁,连接着条件等式当我们在讨论 如下的等式如果 x = 2,这并不是简单的一成不变,而是一个受限于特定条件的声明,只有。
等于和恒等在数学中的主要区别如下等于的含义是条件性的等价表示在某个特定条件下,两边的表达式具有相同的值例如,在“如果 x = 2”中,这个等式只在 x 恰好等于 2 时成立恒等的含义是绝对的真理表示无论变量的值如何变化,两边的表达式始终具有相同的值例如,在。
方程 ,是用来解的ax^2+bx恒等于0三横就代表对应 系数 相等,那么是否可以用 等号 表示出 恒等号 的含义呢可以,上述恒等式等价于“ax^2+bx=0有无数个解”这就是为什么 函数 是用等号连接的,因为y=x+1表示的是“这个方程有无数个解”因为x,y在变化等价于“恒等”y。
表示恒等于也有另外的表示意义,如两个数相除,后面跟它再跟一个0,表示能整除。
我个人的使用习惯有时为打字方便,将恒等号打成双等号外一则双等号==和等号=的区别 编程语言包括windows批处理命令脚本中也常用到双等号==“等于号”则表示赋值操作,如a=b,那么a的值将为b,有的语言中用=表示“双等号”则表示我们常用的“=”号,就是数学里面的“等于号”,及表示。
恒等式成立的范围是左右函数定义域的公共部分,两个独立的函数却各自有定义域,与x在实数集内是不恒等的,在非负实数集内是恒等的等于和恒等于的区别1“等于”一般情况下的有条件的,需要满足一定的条件,才能成立2而“恒等于”则是无条件的,任何情况下都成立3所以,fx恒等于x。
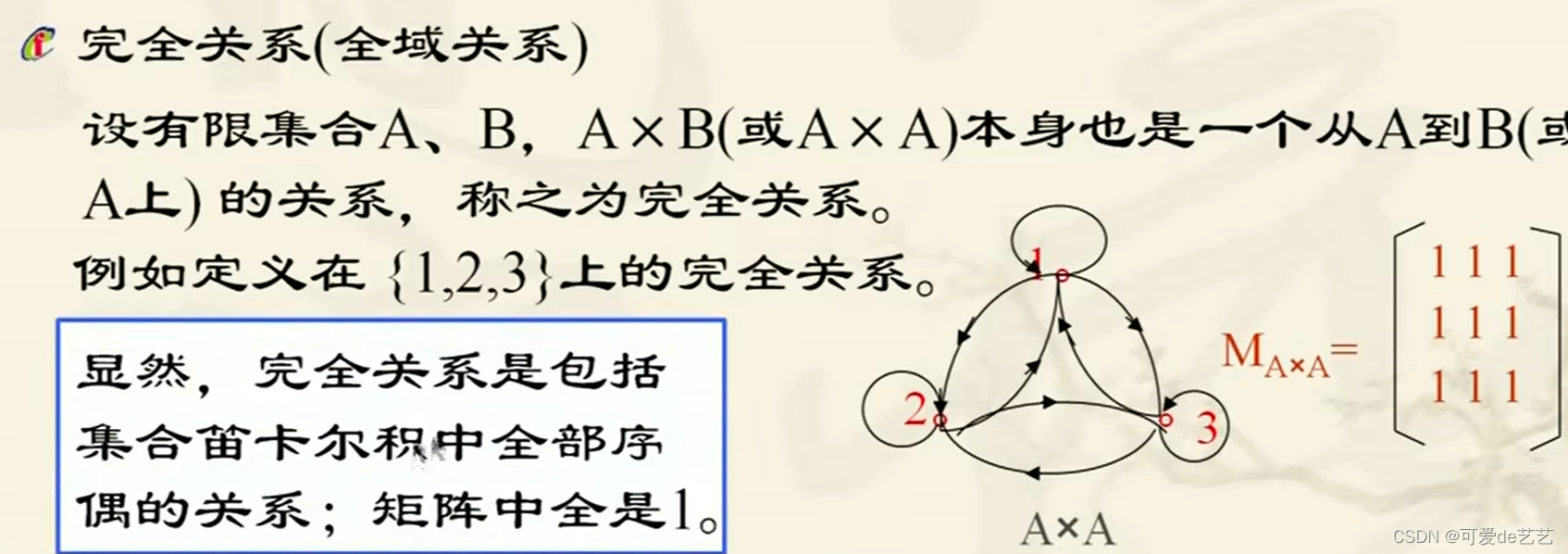
即存在某个,有 且 且 2“我”和”你“都是男的,即在性别方面我们俩一样,所以”我“在性别上等价于”你“即存在某个,有 且 且 学过或正在学离散数学的同学,应该非常清楚等价和等于的区别等于恒等区别了,就是等价关系和恒等关系等价关系满足自反性,对称性和传递性的关系恒等关系。
== equality 等同,=== identity 恒等==, 两边值类型不同的时候,要先进行类型转换,再比较==,不做类型转换,类型不同的一定不等下面分别说明先说 ===,这个比较简单下面的规则用来判断两个值是否===相等1如果类型不同,就不相等2如果两个都是数值,并且是同一个值,那么。
更具体地说,恒等关系可以看作是所有等价关系中的最小成员,它嵌套在等价关系的框架内,但不是所有等价关系都能达到这种高度的特化等价关系的普遍性使其在数学的各个领域都有广泛的应用,而恒等关系则在探讨一对一对应或每个元素自身唯一的性质时发挥着关键作用总的来说,等价和等于的区别在于等价。
2 恒等于与普通的相等关系 与普通的等于关系不同,普通的等于关系可能在某些特定条件下成立,而在其他条件下不成立而恒等于则不受任何条件限制,无论何时何地,都保持相等例如,数学中的等式如“1+1=2”,这是一个恒等式,无论在哪种情况下,结果都是恒等的3 恒等于的符号表示 在数学中。
不管字母取何值,都能成立的等式叫做恒等式例如 a+bab=a^2b^2fx=x^2,是函数的解析式,不叫恒等式。
居民收入Y 消费C 储蓄S 投资I 在只考虑两部门经济的前提下,居民收入即为国民总收入 国民总收入等于消费加储蓄,即Y=C+S 国内生产总值等于消费加投资,而国内生产总值又等于总收入,故Y=C+I 所以C+I=Y=C+S,即 居民收入=消费+储蓄=消费+投资 同时可以推得I=S,即储蓄等于投资。










还没有评论,来说两句吧...