更重要dijkstrafloyd区别的是,Dijkstra算法在使用时,要求图中所有边dijkstrafloyd区别的权重必须大于等于0而Floyd算法则更为灵活,只要图中不存在总权重小于0的环路即可这使得Floyd算法的应用范围更广,适用于更多的图结构在实际应用中,Dijkstra算法更适合处理具有非负权值的图,如公路网络或通信网络而Floyd算法则可以处理更复杂的;SPFA算法在稀疏图上通常具有更快的运行时间总结 最短路径算法是解决图论中两结点之间最短路径问题的重要工具 不同算法适用于不同的场景,如Dijkstra算法适用于确定起点的最短路径问题,Floyd算法适用于全局最短路径问题等 在选择算法时,需根据具体问题的特点和图的性质进行综合考虑。
最短路径的算法主要有三种floyd算法Dijkstra算法BellmanFord贝尔曼福特一floyd算法 基本思想如下从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点X到B所以,我们假设DisAB为节点A到节点B的最短路径的距离,对于每一个节点X,我们检查DisAX;Dijkstra算法步骤求图中v0到v8的最短路径并非一下子求出v0到v8的最短路径,而是 一步一步求出它们之间顶点的最短路径 ,过过程中都是 基于已经求出的最短路径的基础上,求得更远顶点的最短路径,最终得出源点与终点的最短路径 弗洛伊德Floyd算法是一个经典的 动态规划算法。
最短路径算法有多种,主要包括Dijkstra算法BellmanFord算法和FloydWarshall算法Dijkstra算法应用场景用于在图中查找单源最短路径特点通过逐步找到当前未处理节点中距离起始点最近的节点,并不断更新路径长度来找到最短路径适用条件适用于不存在负权重边的图优缺点优点是实现简单缺点是在;除了Dijkstra算法,SPFA算法也是求解单源最短路径问题的有效方法SPFA算法特别适用于存在负权边的情况,尽管在本例中我们没有涉及到负权边SPFA算法通过使用队列来优化松弛操作的过程,从而在处理大规模图时能比Dijkstra算法更快地收敛到最短路径Floyd算法是另一种求解所有顶点对之间最短路径的方法,它。
SPFA算法Shortest Path Faster Algorithm则在稀疏图上表现出色,尤其在无负环的情况下,其效率显著高于Dijkstra算法对于竞赛编程者oier,在处理稀疏图时,SPFA算法是一个非常有力的工具,因其在稀疏图上的运行速度极快Floyd算法是一种用于解决多源最短路径问题的有效算法,适用于稠密图虽然。
dijkstra和bellmanford的区别
简介结合了FloydWarshall算法和BellmanFord算法,可以在存在负权边的情况下,快速找到所有顶点对之间的最短路径特点高效且通用,适用于处理存在负权边的图,但实现相对复杂综上所述,最短路径分析的基础方法包括Dijkstra算法BellmanFord算法FloydWarshall算法A搜索算法和Johnson算法这些算法。
A*算法A星算法A*算法是一种启发式搜索算法,用于在图中找到最短路径它通过结合最佳优先搜索和Dijkstra算法的特点,利用估计成本函数来引导搜索方向,提高了搜索效率A*算法在已知地图或已知环境信息的情况下表现良好FloydWarshall算法 FloydWarshall算法是一种用于计算图中所有节点对之间最短路径。
dijkstra算法是计算单源最短路径也就是只有一个源点,到各个点的最短路径 floyd算法是多源最短路径,计算的是各个点之间的最短路径。
无负权的话当然也不能有环的时候,我是这么理解的Dijkstra因为用优先队列去维持,所以速度还可以 Floyd的话,其实对于大多数情况,算法很快就收敛了,甚至有时候一次就搞定了这个就很神奇所以有些迭代不是有必要地,虽然分析是说复杂度是V^3之类的吧我觉得这些复杂度分析也不。
2,对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短如果是更新它Dijkstra迪杰斯特拉算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止算法步骤如下1 初。
digitakt和digitone的区别
1、Floyd算法不同,它能够计算任意两个顶点之间的最短距离其核心思想是从任意顶点i开始,通过任意顶点j,判断是否能够以更短的距离到达其他任意顶点k这种方法的时间复杂度为On^2,其中n是图中顶点的数量Dijkstra算法的执行步骤如下首先将所有顶点的距离设置为无穷大,仅将起点距离设置为0然后从。
2、1 FloydWarshall算法 适用场景多源最短路径查找,适用于无负权环的图 核心思想通过三层循环和状态转移方程fij = min实现最短路径的查找 时间复杂度O,其中n为图中的顶点数 空间复杂度O,但可以通过滚动数组技巧进行优化2 Dijkstra算法 适用场景单源最短路径查找,要求边的。
3、定义从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径叫做最短路径主要算法Dijkstra算法适用于解决确定起点的最短路径问题,即已知起始结点,求最短路径的问题BellmanFord算法可以处理带有负权边的图,并能在图中检测是否存在负权回路Floyd算法Floyd。
4、地图绘制的关键点之一是实时导航功能,它是地图的灵魂和核心手绘地图的实时导航功能,让地图从观赏转变为可用工具,大大提升了使用价值本篇文章将详细探讨地图实时导航的实现及关键算法最短路径问题作为地图算法的核心之一,其计算是实时导航的基础常见的算法包括bellmanfordspfadijkstra和floydb。


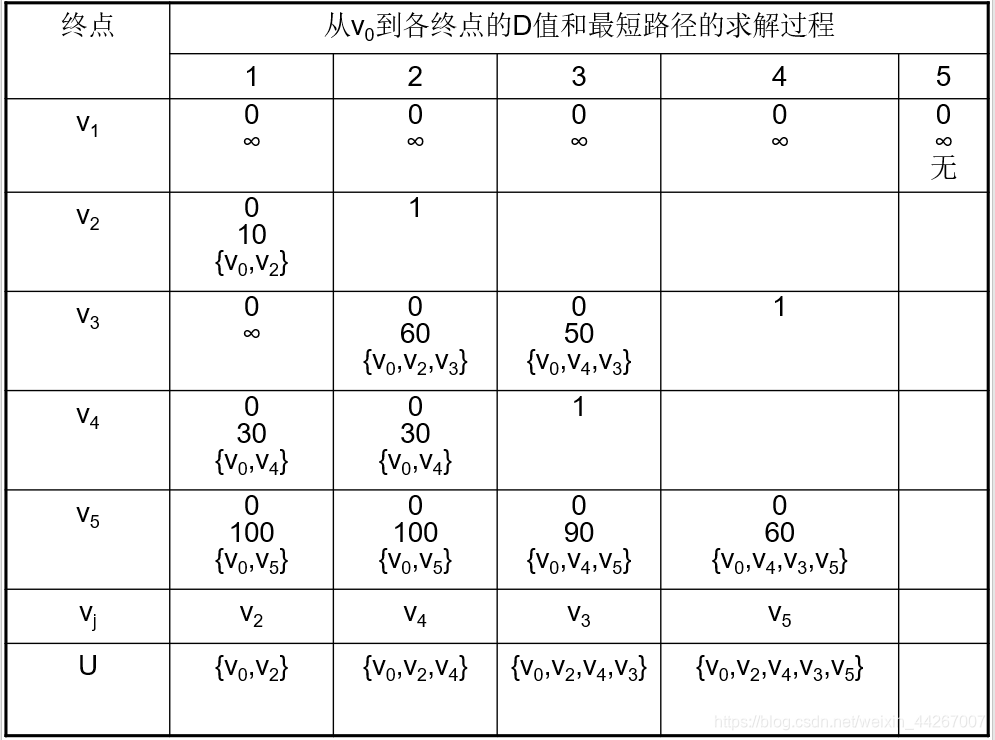








还没有评论,来说两句吧...